the curse of dimensionality
"im an ml guy I should be writing more about ml"
The Curse of Dimensionality is one of my favorite concepts within machine learning. It’s actually what got me into the field, so if you are just starting your career as an ML practitioner or you’re a top tier AI engineer maybe this article will be an interesting read for you.
What does “The Curse of Dimensionality” mean?
So the CoD is an encapsulation of properties that occur at high dimensional space. It’s particularly important when learning from data because we are dealing with high dimensions (think images, 3d structure, etc). The “curses“ are basically the problems that arise once we are in the high dimensional space. Usually when we talk about this we are referencing feature representations rather than data inputs themselves but this can also be a problem, as the saying goes “garbage in garbage out“
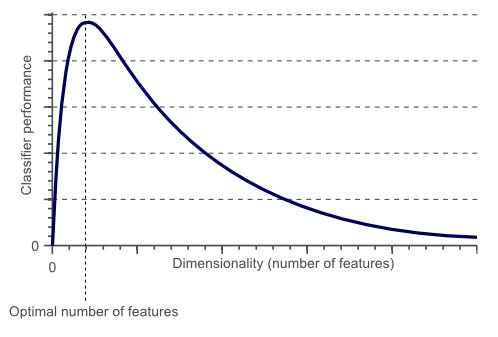
Another term that is relevant is “Hughes phenomenon“. In short the idea is that the predictive power of a model increases as the number of dimensions are increased (using the same data size) but there is a threshold to the dimensionality, which if reached, begins to deteriorate the power of the model. That threshold crossing is where we begin to see the effects of the CoD.
A Few Curses
Sparsity
With high dimensions we may introduce data sparsity. Sparsity in general is bad news across many parts of data learning process. It makes computation more expensive, pattern learning is negatively impacted, and overfitting can happen because the model essentially starts learning the noise that comes from sparse data.
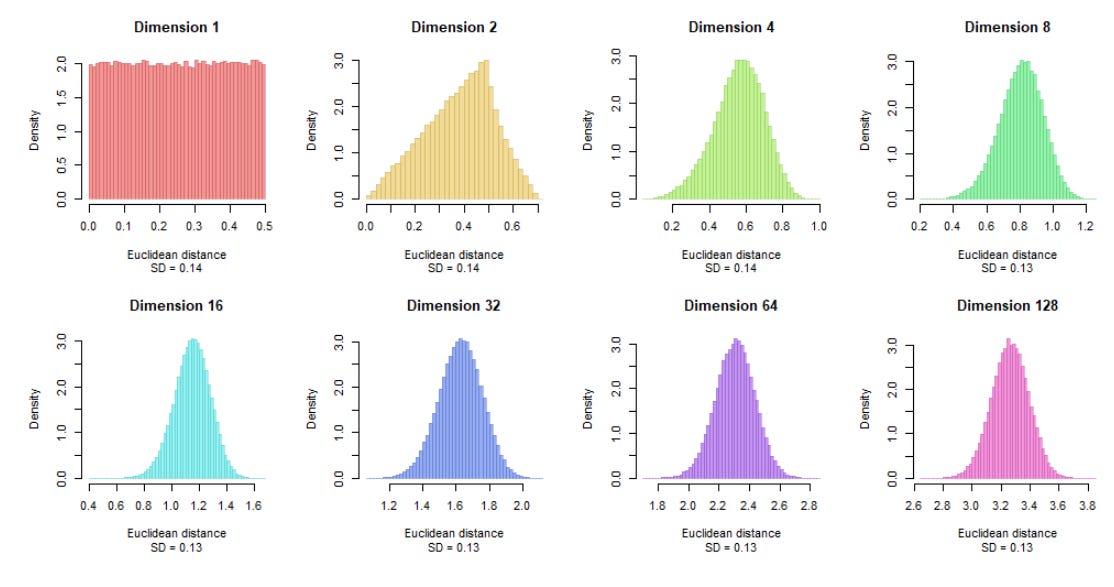
Distance Homogenization
Meaning that the distances between points are all converging to a similar value so a distance loses its value. This is bad if you want to do things like semantic search. The reason the points converge distances at high dims is because
Potential Solutions
Luckily there are ways around a lot of these problems and it's usually just good practice to employ some of these when working with high-dim data (which these days is normal). Probably one of the more obvious ones on people’s minds is dimensionality reduction via something like PCA/t-SNE etc. This is good but can sometimes lead to loss of information (which makes sense since you’re taking a space thats able to hold more information on essentially shrinking it), through experimentation though you can be successful.
There’s also an entire field dedicated to feature selection which can reduce a lot of the issues described above. People are quite interested in managing this in a way that the get the most expressive features out of their models. Often times people are using regularization techniques during learning to avoid a lot of the aforementioned problems, this is also, an entire field.
The Blessing Of Dimensionality
There are also some benefits to high-dim representation! This is actually new to me as I’ve always believed that high-dim should be avoided if you can in a classical machine learning sense. David Donoho introduced this term and the idea is basically a counterpoint to the issues listed above. High dimensions is good. Because the higher the dimension the more information we can take advantage of to learn patterns. If you were to try and reduce the space then you just have less information to learn from. So it’s not really always a good thing to trim things down for performance gain, but as with many “concepts“ this balance is a whole field on its own.